Parameterized Pooling Layers

TLDR: This blog will discuss:
1 - Two parameterized pooling layers which aim to improve beyond average and max pooling
2 - The techniques introduced are: AutoPool and Generalized Mean Pooling (GeMPool)

1 - Introduction

Pooling layers in deep learning serve the purpose of aggregating information - given a bunch of numbers, how do I summarize them into 1 number which represents this bunch of numbers the most?

The very first encounter of most deep learning practitioners with pooling layers should be within the stack of “conv - pool - relu” block in image classification architectures, e.g. LeNet, ResNet, etc. Pooling layers come after convolution layers, with the purpose to downsample the image, also hoping to produce a more compact representation within a lower dimension. Another common usage of pooling layers is on temporal aggregation for sequence data, e.g. summarizing values across a time axis. For example, to learn an embedding (e.g. song embedding, sentence embedding) of shape $(d,)$ from a 2-D sequence data (e.g. spectrograms, word embeddings) with shape $(M, T)$, where $T$ is the temporal axis, it is very common to apply pooling on the temporal axis to reduce the representation into 1-D.

The most common pooling methods are either average pooling or max pooling. Average pooling takes the mean of a given set of values, hence the contribution of each value to the final aggregated value is equal. Whereas, max pooling takes only the max value, hence the max value contributes fully to the final aggregated value. A (probably inappropiate) analogy will be: average pooling is more like collective opinion & democracy, whereas max pooling is more like tyranny & eliticism where only the best speaks.

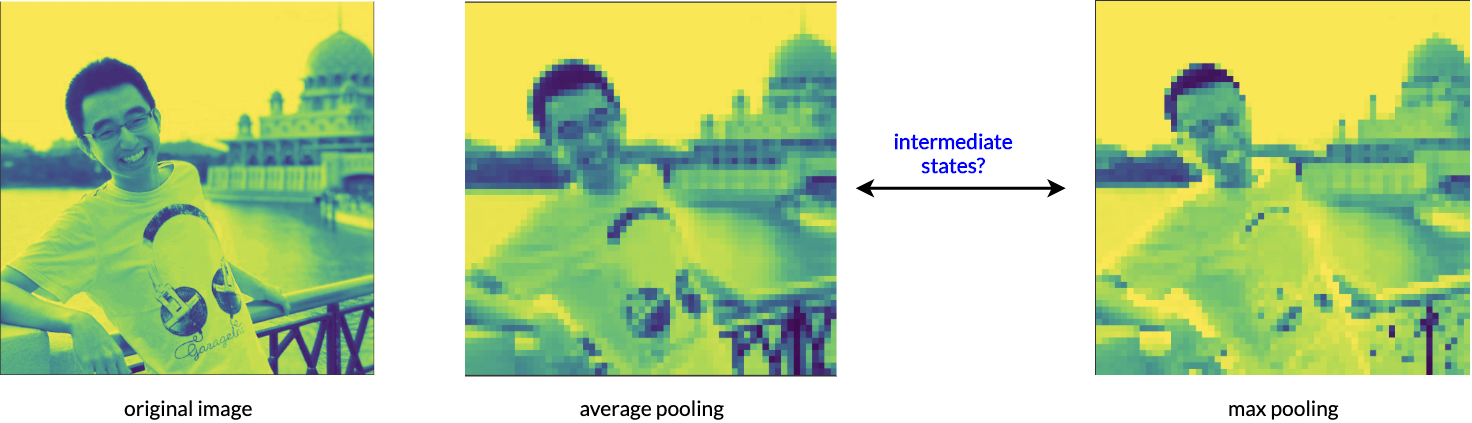
Figure 1: Average Pooling VS Max Pooling. Is there a way to exploit states between both?

The also explains why average pooling produces smoother, blurrer feature maps, and max pooling produces sharper, discontinuous feature maps. However, it is not guaranteed that either of the representation is the best for our applications. The question is: is there a way to exploit states between average and max pooling? Furthermore, can we rely on backpropagation and deep learning to learn a parameter $p$, such that it gives us the best pooled output for our own application? This is the motivation of parameterized / adaptive pooling methods.

Below I will discuss two methods that I recently read up, which is AutoPool and Generalized Mean Pooling (GeMPool). Both methods are commonly used in papers across signal processing, MIR, and image recognition applications.

2 - AutoPool

AutoPool, proposed by McFee et al, generalizes the pooling equation as below:

$$w(\alpha, x) = \frac{e^{\alpha \cdot x}}{\displaystyle\sum_{z \in X} e^{\alpha \cdot z}} \\ y = \displaystyle\sum_{x \in X} x \cdot w(\alpha, x)$$

where $y$ is the aggregated value, $X$ is the set of values, and $\alpha \in [0, \infty)$ is the trainable scalar parameter.

We can easily see that this equation takes the form of a weighted sum - each element $x$, contributes to the final aggregated value $y$, with a weight factor determined by function $w$.

when $\alpha = 0$, it is clear that $w(\alpha, x) = \frac{1}{|X|}$ because $e^{\alpha \cdot x} = 1$ and the denominator resembles the number of elements in $X$. The corresponds to average pooling, and each value has equal contribution.
when $\alpha = 1$, the authors term this as softmax pooling, as each value contributes with a factor of its softmax value.
when $\alpha \to \infty$, the max value will have more contributing factor. This is because $$\displaystyle\lim_{\alpha \to \infty} \frac{e^{\alpha \cdot x}}{\displaystyle\sum_{z \in X} e^{\alpha \cdot z}} =
\displaystyle\lim_{\alpha \to \infty}
\frac{ (\frac{e^{\alpha \cdot x}}{e^{\alpha \cdot x_{max}}}) } { 1 + (\frac{e^{\alpha \cdot x_1}}{e^{\alpha \cdot x_{max}}}) + (\frac{e^{\alpha \cdot x_2}}{e^{\alpha \cdot x_{max}}}) + … }$$ Hence, by dividing $x_{max}$ on both numerator and denominator, we can see that only if $x = x_{max}$, then the limit equals to $1$, or else the limit equals to $0$. We can see that this corresponds to max pooling.

2 - Generalized Mean Pooling (GeMPool)

GeMPool, first proposed by Radenovic et al., generalizes the pooling equation as below:

$$y = (\frac{1}{|X|} \displaystyle\sum_{x \in X} x^p)^{\frac{1}{p}}$$

where $y$ is the aggregated value, $X$ is the set of values, and $p \in [1, \infty)$ is the trainable scalar parameter.

when $p = 1$, this clearly corresponds to average pooling;
when $p \to \infty$, it corresponds to max pooling. A way to prove this is to calculate the following limit:
$$ \lim_{p \to \infty} (\frac{1}{|X|} \displaystyle\sum_{x \in X} x^p)^{\frac{1}{p}} = \lim_{p \to \infty} (\frac{1}{|X|})^\frac{1}{p} \cdot x_{max} \cdot ((\frac{x_1}{x_{max}})^{p} + (\frac{x_2}{x_{max}})^{p} + …)^\frac{1}{p} = x_{max}$$

3 - Other Aggregating Mechanisms

Both methods aforementioned are parameterizing pooling methods with a single scalar value. We find the common design of such equation is to parameterize the exponent of the equation. We see that when the exponent is at its base value, the equation falls back to average pooling. As the value of exponent is increased, we can see that the contributing factor of large values increase, where for small values the contributing factor decreases. Several papers and applications have conducted ablation studies that show parameterized pooling improves model performance, but comparison across different parameterized pooling methods hasn’t been conducted before to the best of my knowledge.

A more sophisticated method of aggregating values is to use attention, as a weightage is learnt for each value, known as attention mask, however the amount of parameters on the aggregation also scales up w.r.t the size of values. It will be exciting to see if pooling mechanisms and attention mechanisms could be compared side-by-side in terms of bringing improvement to model performance.

4 - Code Implementation

I provide the portals to the original source code / reimplementation of the parameterized pooling methods: