The power function \(x^y\) is integral to many DSP applications, such as dB to linear gain conversion (\(y = 10^\frac{x}{20}\)), and semitone to Hz conversion (\(f_t = f_0 \cdot 2^{\frac{t}{12}}\)). When studying the code in Dexed, an FM synth modelled over DX7, I find many use cases of the exp2 function (\(2^x\)), especially in the amplitude envelope calculation.

In this post, we will look at how \(2^x\), or the exp2 function, can be approximated for speed-intensive, precision-tolerant use cases. Note that we only discuss the case of exp2, because it is a convenient base in floating point representation (more on this later), and it is easily extendable to the generic power function \(x^y\). Given \(f(k) = 2^k\), we can transform the power function by multiplying a constant \(\log_{2}{x}\) on the input to make use of \(f(\cdot)\):

$$x^y = 2^{y \cdot \log_{2}{x}} = f(y \cdot \log_{2}{x})$$

Initial ideas

A straightforward approach is to truncate the Taylor series of \(2^x\) up to the \(n\)-th term. One can get the Taylor series of \(2^x\) as:

$$2^x = e^{x \ln 2} = 1 + \frac{x \ln 2}{1!} + \frac{(x \ln 2)^2}{2!} + \frac{(x \ln 2)^3}{3!} + … $$

However, to get a good approximation across a wide input range, it requires higher order of polynomials, which is computationally intensive.

Another idea from Dexed is to use a finite-range lookup table and fixed-point arithmetic, however this method is usable only for fixed-point systems.

To get a more precise and efficient implementation in floating point, we need to first understand the floating point representation.

Separating the integer and decimal part

Let’s say we want to implement an exp-2 approximation for a single-precision (32-bit) floating point system. According to IEEE-754 floating point representation, it consists of 1 sign bit, 8 exponent bits, and 32 mantissa (or fractional) bits, as depicted in the diagram:


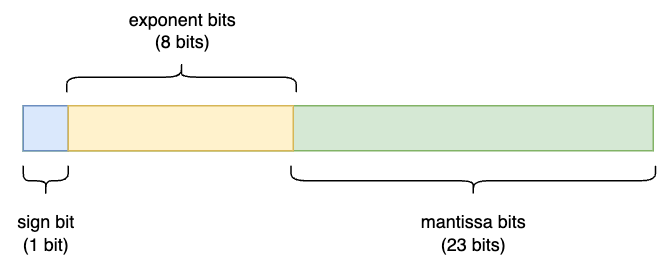
Figure 1: IEEE-754 single-precision floating point format.

The corresponding formula of single-precision floating point is \((−1)^{S} × 1.M × 2^{(E − 127)}\). From this formula, we can observe that: given an integer input, calculating exp2 is essentially bit-shifting to get the exponent bits \(E\). We also need to add the bias value in the exponent bits before bit-shifting. For single-precision, the bias value is 127 or 0x7f, as shown in the formula above.

This gives us an idea of how we can tackle the approximation separately, given an input \(x\):

  • for the integer part \(\lfloor x \rfloor \), bit-shift to the exponent bits;
  • for the decimal part \(x - \lfloor x \rfloor \), use a rational approximation;
  • multiply the output of both parts \(2^{x} = 2^{\lfloor x \rfloor} \cdot 2^{x - \lfloor x \rfloor}\) (in C++, we can use ldexp)

Rational approximation of exp2f

Depending on the rounding mode used to extract the integer part, the range of the decimal part would either be within \([-0.5, 0.5]\) or \([0, 1)\). With this, we only need an approximation precise enough within this range, which is more achievable.

There are a myriad of ideas on how this approximation could be achieved. We can start from an n-th order polynomial approximation. For example, with the help of np.polyfit we can get a 3rd-order polynomial approximation:

$$ 2^{x} \approx 0.05700169x^{3}\ + 0.24858144x^{2} + 0.69282515x + 0.9991608, \quad x \in [-1, 1]$$

This is actually quite close to the Taylor’s expansion at order 3:

$$ 2^{x} \approx \frac{(x \ln 2)^3}{3!} + \frac{(x \ln 2)^2}{2!} + \frac{x \ln 2}{1!} + 1 $$

$$ \quad \quad \quad \quad \quad = 0.0555041x^{3}\ + 0.2402265x^{2} + 0.693147x + 1 $$

The Cephes library uses a Padé approximant in the form of:

$$ 2^{x} \approx 1 + 2x \frac{P(x^2)}{Q(x^2) - xP(x^2)}, \quad x \in [-0.5, 0.5]$$

$$ P(x) = 0.002309x^{2}+20.202x+1513.906 $$

$$ Q(x) = x^{2}+233.184x+4368.211 $$

From a blog post by Paul Mineiro, it seems like the author also uses something similar to Padé approximant, but with a lower polynomial order:

$$ 2^{x} \approx 1 + \frac{27.7280233}{4.84252568 - x} − 0.49012907x − 5.7259425, \quad x \in [0, 1)$$

Timing and Accuracy

We report the absolute error of each approximation method within a given input range. Test script here.

Within input range of \([0, 1)\), 10000 sample points:

max min avg
3rd-order polynomial \(\quad 2.423 \times 10^{-3} \quad\) \(\quad 1.192 \times 10^{-7} \quad\) \(\quad 6.736 \times 10^{-4} \quad\)
Mineiro’s method \(\quad 5.829 \times 10^{-5} \quad\) \(\quad 0 \quad\) \(\quad 2.267 \times 10^{-5} \quad\)
Cephes’ method \(\quad 2.384 \times 10^{-7} \quad\) \(\quad 0 \quad\) \(\quad 2.501 \times 10^{-8} \quad\)

Within input range of \([-0.5, 0.5]\), 10000 sample points:

max min avg
3rd-order polynomial \(\quad 8.423 \times 10^{-4} \quad\) \(\quad 5.960 \times 10^{-8} \quad\) \(\quad 4.764 \times 10^{-4} \quad\)
Mineiro’s method \(\quad 4.995 \times 10^{-5} \quad\) \(\quad 0 \quad\) \(\quad 1.623 \times 10^{-5} \quad\)
Cephes’ method \(\quad 1.192 \times 10^{-7} \quad\) \(\quad 0 \quad\) \(\quad 1.798 \times 10^{-8} \quad\)

We also measure the total time taken to run on 10000 sample points, averaged across 5 runs:

in secs
3rd-order polynomial \(\quad 4.747 \times 10^{-5} \quad\)
Mineiro’s method \(\quad 8.229 \times 10^{-5} \quad\)
Cephes’ method \(\quad 4.854 \times 10^{-4} \quad\)

We can see Cephes provides the best accuracy, while 3rd-order polynomial approximation provides the best speed. Mineiro’s method keeps the absolute error within the order of magnitude \(10^{-5}\), while using only ~20% of the time needed by Cephes.

Code example in SIMD

SIMD is commonly used to provide further computation speedup on CPU. The aim of of this post is also to find an efficient SIMD implementation for exp2, which is still lacking in common SIMD operation sets. Below we will look at an example of exp2 approximation implemented using SSE3. We use the 3rd-order polynomial approximation below:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
__m128 fast_exp_sse (__m128 x)  {
    __m128 x_int_f, x_frac, xx;
    __m128i x_int;

    __m128 c0  = _mm_set1_ps (0.05700169f);
    __m128 c1  = _mm_set1_ps (0.24858144f);
    __m128 c2  = _mm_set1_ps (0.69282515f);
    __m128 c3  = _mm_set1_ps (0.99916080f);

    // obtain the integer and fractional part
    x_int = _mm_cvtps_epi32(x);
    x_int_f = _mm_cvtepi32_ps(x_int);
    x_frac = _mm_sub_ps(x, x_int_f);

    // perform 3rd-order polynomial approximation on fractional part
    xx = _mm_mul_ps(x_frac, c0);
    xx = _mm_add_ps(xx, c1);
    xx = _mm_mul_ps(x_frac, xx);
    xx = _mm_add_ps(xx, c2);
    xx = _mm_mul_ps(x_frac, xx);
    xx = _mm_add_ps(xx, c3);

    // compute 2^n for integer part through bit-shifting and adding to exponent field
    x_int = _mm_add_epi32(x_int, _mm_set1_epi32(0x7f));
    x_int = _mm_slli_epi32(x_int, 23);
    x_int_f = _mm_castsi128_ps(x_int);

    // compute final result, 2^n = (2^i)(2^f)
    xx = _mm_mul_ps(xx, x_int_f);

    return xx
}

Some notes to discuss:

  • For the integer rounding part, _mm_cvtps_epi32 is used, which is a float-to-int casting. To use round-to-nearest mode, we can use _mm_round_ps, but it is only supported in SSE4.1.

  • There is a difference between type conversion _mm_cvtps_epi32 and reinterpret casting _mm_castsi128_ps. Type conversion converts a fixed point integer representation to a floating point representation, and retain its value. Reinterpret casting takes the byte pattern of the fixed-point input, and reinterprets it based on the floating point representation.

  • Padé approximant can be used by replacing lines 16-21, and would require the division operator _mm_div_ps.

References

  1. Creating a Compiler Optimized Inlineable Implementation of Intel Svml Simd Intrinsics

  2. Added vectorized implementation of the exponential function for ARM/NEON

  3. Fastest Implementation of the Natural Exponential Function Using SSE

  4. exp-2 in torch-cephes library

  5. Fast Approximate Logarithm, Exponential, Power, and Inverse Root

  6. fastapprox

  7. Where does this approximation for 2^{x} − 1 come from?